Eppen a racsos tartoknak neztem utana (tetoszerkezetek erdekeltek) a neten, ahol megemlitettek a Cremona diagrammot. Nem emlekszem, hogy az egyetemen lett volna szo rola, ott csak a reszekre bontasos modszerrel foglalkoztunk.
A Cremona diagramm egy grafikus modszer a a sikbeli racsos tartok elemeiben ebredo erok meghatarozasara. Luigi Cremona olasz matematikus talalta ki.
Az erok meghatarozasanak menete:
Eloszor felrajzoljuk a reakcioeroket valamint a terheleseket vektorosan egy alkalmasan megvalasztott meretarany szerint. Ezen erok egyuttes eredoje nulla, mivel a rendszer nyugalomban van.
Ugyan ez az allitas all a racsos tarto minden egyes csomopontjara is. Mivel a kulso terheleseken es a reakcioerokon kivul minden csomopontban az erok rudiranyuak, nagyon egyszeru kiszerkeszteni a tobbi erot. Lassuk peldakon keresztul mirol is van szo:
Az elso peldaban a legegyszerubb racsos tartot, egy harom rudbol allo haromszoget vizsgalunk meg. Fuggoleges iranyu terheles van a C pontban, igy a reakcioerok is fuggolegesek lesznek.
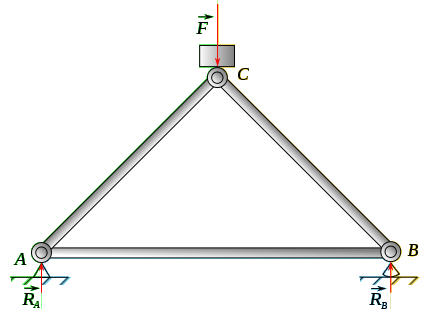
Az erok az egyes elemekben a kovetkezokeppen alakulnak:
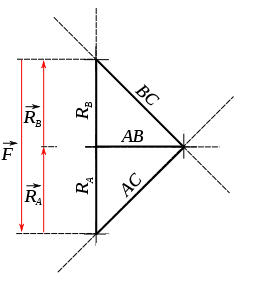
A masodik peldaban egy kicsit bonyolultabb racsos tartot elemzunk. Kek nyilakkal jeloltek a nyomott, pirossal a huzott elemeket. A tarto felvesz fuggoleges es vizszintes terhelest is.
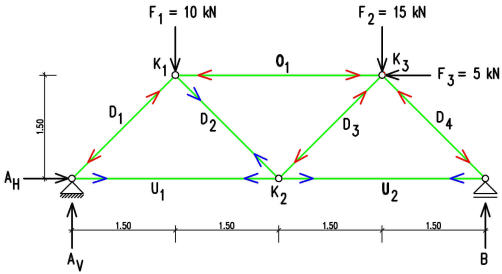
Jol lathato, hogy a B, Av, Ah, F1 es F2 erok egy zart teglalapot alkotnak, eredojuk nulla.
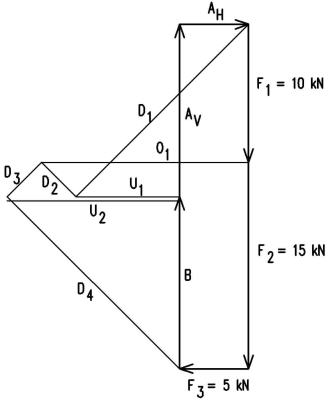
Bar a fenti kepen rajta van a megoldas, erdemes megnezni az elso lepest:
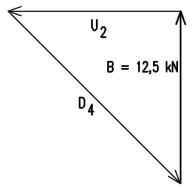
A jobb oldali tabasznal ismert a B reakcioero, es a ket rudiranyu ero (U2 es D4) iranya. Ebbol ki lehet szerkeszteni a U2 es D4 nagysagat.
Ezzel a modszerrel vegig lehet menni a bal oldali tamaszon, majd az osszes tobbi csomoponton is.
Megjegyzes:
Ahhoz hogy a sikbeli racsos szerkezet stabil legyen, haromszogekbol kell legyen osszerakva. Matematikailag megfogalmazva:
m>=2j-r
m: az elemek szama
j: a csomopontok szama
r: lekotott szabadsagfokok szama
Ha egyenloseg all fent, akkor statikailag hatarozott a tarto, ha m>2j-r akkor hatarozatlan.
